[Geometry] Archimedes' Triumph
By: Tao Steven Zheng(鄭濤)
【Problem】
In Volume I of On the ''Sphere and the Cylinder'', Archimedes (c. 287 - 212 BC) determined the volumetric ratio of a sphere to a circumscribed cylinder. The height and width of the cylinder is equal to the diameter of the sphere. What is this ratio?
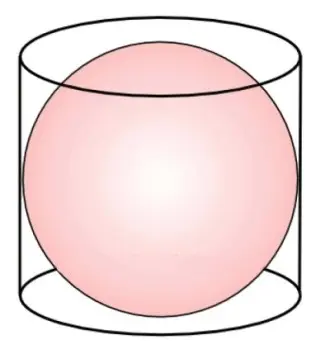

【Solution】
Let the radius of the sphere be . The circumscribed cylinder shares the same height and width as the sphere, so?the height of the cylinder is
.
The volume of a sphere is , and the volume of a cylinder is
. Thus, the volume circumscribed cylinder is
Therefore, the volumetric ratio of a sphere to its circumscribed cylinder is
which simplifies to

標(biāo)簽:

