Electric Fields around Conductors||Electromagnetism

//In this chapter we focus on field and potential due to charges on conductors, where charges are free to move around.
//Let's start it.

1. Conductors and fields around
Usually materials can be?classified into three classes: conductors, semi-conductors, and insulators.?A conductor contains free charges that can move around?under the influence of electrostatic force. In the interior of such a conductor, in the static case, if there's only Coulomb forces acting on charge carriers inside, the electric field inside must be 0.
Otherwise, the free?charge carriers would experience a force and would be thereby set in motion, and thus we would not have a static situation after all.
(Well I find?this part?extremely difficult?to conclude briefly...)
To be precise, we can make the following statements about any such system of conductors, whatever their shape and arrangement:
for every point inside the material of a conductor.
(Constant) at all points inside the material and on the surface of the same?conductor.
At any point just outside a conductor, the electric field is perpendicular to the surface, and is proportional to the electric charge density of the surface,?.
2. Image Charges
//Now I feel it's extremely hard...
To solve electrostatic?problems with conductors, we use image charges. They don't actually exist, but the electric field generated by both real charges and image charges can make the surface of the conductor an equipotential surface, and therefore meet the boundary condition of the conductor.
Two typical examples of image charge:
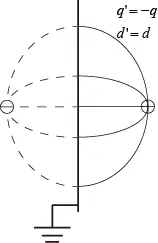
① Image charge generated by a large conducting plain with potential 0.
The image charge will be:
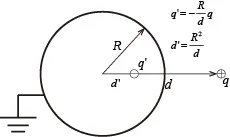
② A conducting sphere with radius R and?potential 0.
The image charge will be:
3. Capacitance and capacitors
The potential of an isolated conductor is proportional to total charge it carries,
We call factor? capacitance of the conductor.
For a simple spherical conductor,
so its capacitance is
If there are two conductors oppositely charged, the system is called a capacitor. If the two conductors?has charge??and potential?
respectively, we have
and constant? is the capacitance of a capacitor.
For example, two large plains with area? are placed closely, separated by a distance?
, we have:
So the capacitance is

Two years ago when I was still in high school, I was studying electromagnetism for PhO competition, and a problem really impressed me. It was given by a professor in USTC (where I failed to reach?at last...):?
Find the capacitance of two orthogonal(正交的) spheres. Radius? respectively.
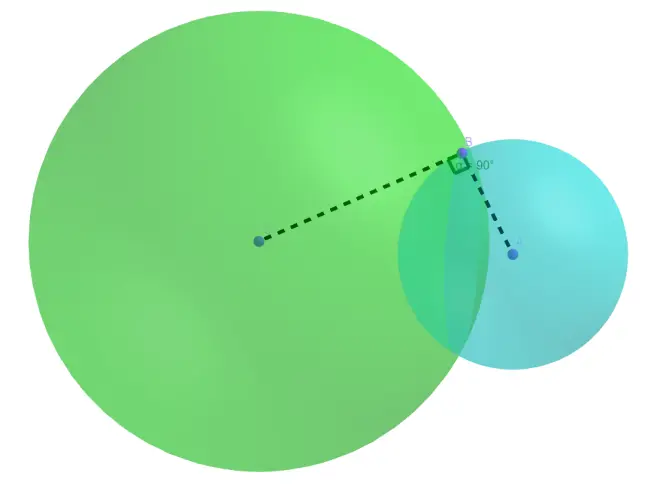
First we put two charges at the center of the two spheres,?. To make the potential on both surface?the same, we have?
.
But conductive objects can be influenced, so both spheres generates image charge to balance the field from the other sphere.
Surprisingly, the image charge of two spheres are actually the same: same amount of charge and same position. Which is
And its position is between the two centers, with distance to two centers
respectively.
So we know the field generated by? can meet the boundary condition.
This is the capacitance of this strange shape. This really impressed me.
4. Energy stored in a capacitor
If we store charges in a capacitor, we do work to the system, so the potential energy of the system increses. Potential energy?:
References
[1] Edward M. Purcell, David J. Morin. Electricity and Magnetism (Third Edition)[M]. Cambridge Univercity Press.